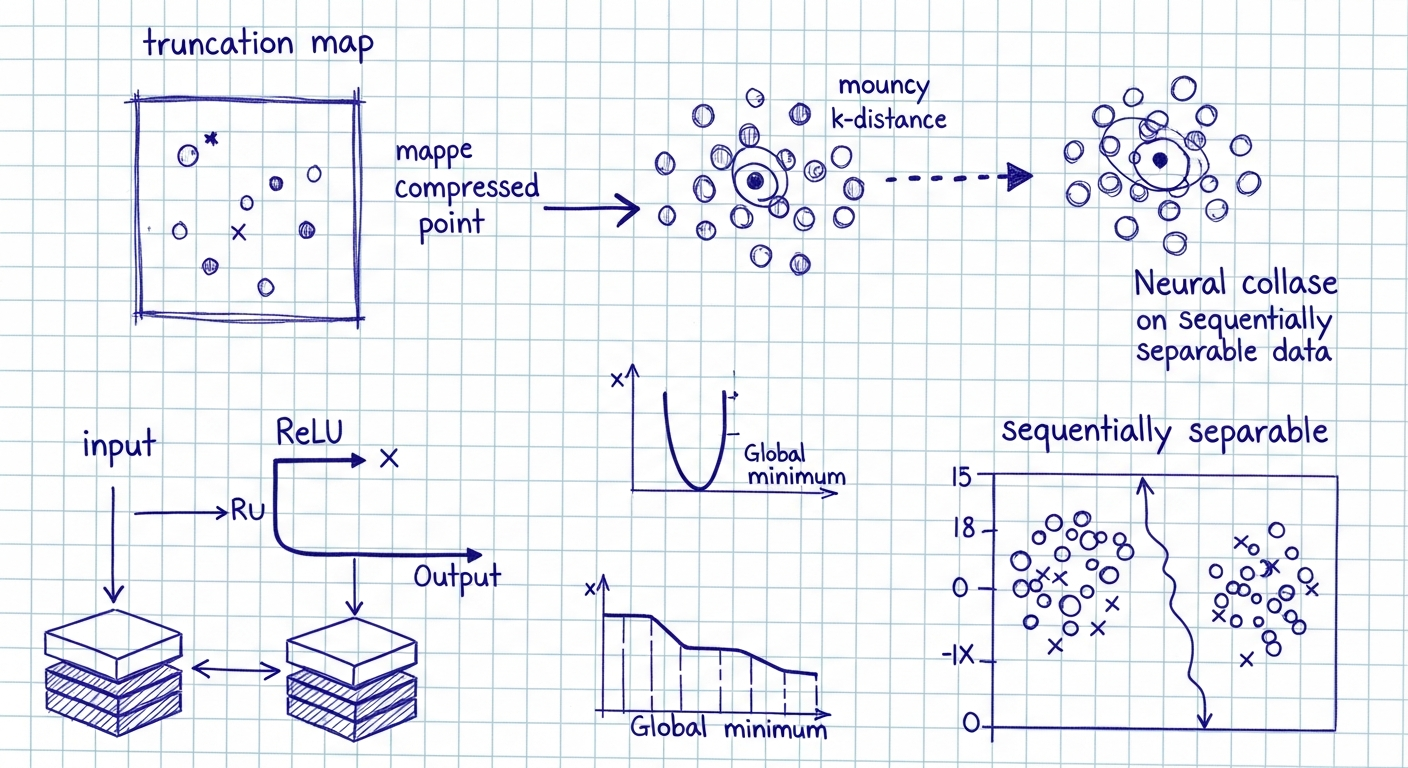
מינימום גלובליים ניתנים לפירוש של רשתות נוירונים עמוקות ReLU על נתונים ניתנים להפרדה באופן סדרתי

העבודה מראה איך לבנות רשתות ReLU שעושות 'אינטרפולציה' מדויקת (אפס אובדן) על סוגי נתונים בעלי מבנה גיאומטרי מסוים, בלי תלות במספר הדוגמאות. המשמעות הפרקטית: אם נתוני האימון מסודרים כקלאסטרים נפרדים או בצורה שניתן לבצע סדרה של הפרדות אחת-על-כולם, אז אפשר לתכנן פרמטרים מפורשים לרשת עמוקה שממפה כל מחלקה לנקודה יחידה ומשלים את הסיווג בשכבה האחרונה. זה שימושי להבנה אינטרפרטבילית של מה השכבות עושות (לדוגמה: השכבות החבויות 'דוחסות' שונות בתוך-מחלקה ואילו השכבה הסופית מפעילה מאפייני least-squares), ולתכנון ארכיטקטורות עם מספר פרמטרים מצומצם שניתן לנתח תיאורטית. בנוסף תובנות אלה מקשרות את התנהגות הרשת לתופעות נצפות כמו "neural collapse" ומספקות כלים לבדיקת מובנות המבנה של מינימיזטורים.

רקע ומטרת המחקר

המאמר חוקר את המבנה הגיאומטרי של מינימיזטורים גלובליים עבור רשתות ReLU בעבודת סיווג רב-מחלקתי. במקום להסתמך על אימון אקראי באמצעות גרדיאנט דסנט, המחקר בונה במפורש משפחות של משקולות והיסטים (biases) המתארות פעולת שכבות ברמה הגיאומטרית על מרחב הקלט. המטרה היא להסביר ולתת תיאור אינטרפרטבילי לשכבות: כל שכבה נתפסת כמפה חיתוך (truncation map) המסוגלת לשמר מקטעי מרחב (forward cone) ולדחוס מקטעים אחרים (backward cone) לנקודה.

מודל, סימון ועקרון המפה החותכת

המחקר מתמקד בארכיטקטורות עם L שכבות: השכבות האחרונות (אפיקיות) הן לינאריות והשכבות החבויות מפעילות ReLU. המפה החותכת עבור משקל W והיסט b מוגדרת כ- τ_{W,b}(x) = W^+ (σ(Wx + b) - b), כאשר W^+ הוא המעריך הכללי (generalized inverse). שימוש ברעיון הפרמטרים המצטברים W^{(l)}, b^{(l)} מאפשר לתאר את השכבות החבויות כשרשרת של מפות τ הפועלות ישירות במרחב הקלט, ואילו השכבה האחרונה היא מיפוי אפרי המיישם התאמה לינארית על תוצאות הטרוקציות.

כלים גיאומטריים: חרוטים וזוויות קריטיות

המאמר מגדיר חרוטים (cones) C_θ[h] סביב וקטור כיוון h וזווית פתיחה θ. לוקח חומר אנליטי על בחירת θ קריטיות: למשל זווית θ_n הגדולה ביותר עבור חרוט שמוטבע ברבע החיובי של R^n היא θ_n = 2 arccos(√(n-1)/√n). הוכח כי ניתן לבחור מטריצות W וביאסים כך שהמפה הטרנקציונית היא זהות על החרוט הקדמי ודוחסת את החרוט האחורי לנקודה בסיסית.

תצורת נתונים 1: נתונים מקובצים (clustered)

הגדרה פורמלית: הנתונים מחולקים ל-Q כיתות עם ממוצעים x_{0,j}, ושוויוני השונות בתוך כל קבוצה מוגבלים על ידי δ קטן ביחס להפרשים בין ממוצעים: δ < c_0 min_j |x_{0,j} - x| כאשר c_0 ≤ 1/4. תחת תנאים אלה ובחירה מתאימה של זוויות ומקדמים μ_j∈(2δ,3δ), ניתן לבנות L = Q+1 שכבות כך שכל אחת מהשכבות תדחס קבוצה אחת לנקודה בזמן שהשאר נשארים ללא שינוי יחסית. מבנה הפרמטרים המצטברים ניתן במפורש: W^{(l)} = I(d0,d_l) W_{θ*} R_l ו-b^{(l)} = -W^{(l)} (x_{0,l}+ μ_l f_l). התוצאה: לאחר Q פעולות τ חוזרות כל מחלקה מומרת לנקודה ושכבת הפלט הלינארית האחרונה ניתנת לפתור ב-LS כך שהאובדן מסתיים ב-0. התכונה המעניינת: המינימיזטור לא תלוי במספר דוגמאות N.

תצורת נתונים 2: סדרתיות הפרדה לינארית (sequentially linearly separable)

הגדרה: קיימת סדרה של כיתות כך שבכל שלב j יש היפר-מישור H_j הנפרד בין הכיתה j לבין (a) נקודות בסיס שנוצרו בשלבים קודמים ו-(b) שאר הכיתות. בעזרת בנייה אינדוקטיבית דומה לקטגוריה המקובצת, בכל שלב מגדירים W^{(l)}, b^{(l)} המבוססים על היפר-מישורים וחרוטים כך שהכיתה המסומנת נדחסת לנקודה pj בעוד אחרות נשארות. אחרי Q שלבים מתקבלות Q נקודות בלתי תלויות לינארית והשלב האחרון פותר בדיוק את משוואת LS: W^{(Q+1)} = Y (X_{red}^{(τ,Q)})^+, b^{(Q+1)} = 0 ומתקבל שוב אובדן אפס. הפרמטרים של שיטת הבנייה ניתנים לפרמטריזציה על ידי: זוויות θ_l, וקטורי נורמל ν_l וקטעים μ_l.

מאפיינים ותוצאות נוספות

• המינימיזטורים שנבנו הם דגנרטיביים (מכיוון שקיימת משפחה של זוויות/פרמטרים שנותנים את אותו אובדן אפס).
• הבנייה עובדת גם אם רוחב השכבות יורד מ-M ל-Q (d_0 = M ≥ d_1 ≥ ... ≥ d_L = Q), ובמקרה אידיאלי ניתן להשיג רשת עם מספר פרמטרים כולל Q(M + Q^2) שמנתחת את הקלט וממפה אותו לסיווג מדויק.
• המפה החותכת מסבירה פונקציונלית את 'דחיסת השונות בתוך-כיתה' (neural collapse NC1) בעוד שהשכבה האחרונה אחראית להתאמת הממוצעים והקונפיגורציה הסופית (NC2, NC3).

השלכות פרקטיות ותובנות תאורטיות

העבודה מספקת מתווה גיאומטרי מפורש להבנת פעולת שכבות ברשתות ReLU: השכבות החבויות יכולות להתפרש כמפות שמטרתן לדחוס שונות פנימית ולהפריד כיתות לפי חרוטים/היפר-מישורים; השכבה האחרונה משלימה התאמה לינארית. הבנייה אינה דורשת ידע בשיטות אופטימיזציה – היא מציגה פתרונות סגורים, ולכן שימושית ככלי להסבר (interpretability) ולניתוח התנהגות איבוד ורכישות כמו neural collapse.

מגבלות וכיווני המשך

התוצאות דורשות מבנה גיאומטרי מסוים בנתונים (קלאסטרים קטנים ומופרדים או סדרתיות הפרדות לינארית). המחקר אינו מציג אלגוריתם לסיכוי/לימוד של פרמטרים אלה מנתונים כלליים, אלא מבנה קונסטרוקטיבי שהוכח תאורטית. כיוונים להמשך כוללים פיתוח אלגוריתמים לזיהוי מצבים בהם תנאי הסדרתיות מתקיימים ושילוב המפות כחלק מאילוף או רגולציה.